真空管の交換時などで出てくるｇｍってなに？（２）

　（１）では、トランジスタを題材にｒｅに付いて説明しました。そしてｇｍとはｒｅの逆数である事、ｇｍが分かるとゲインの計算が簡単（Ｇａｉｎ＝ｇｍＸ ＲＬ）に出来ることを説明しました。
　（２）では、ｇｍに付いて整理した後、プリ管の代表ともいえる１２ＡＸ７真空管での特性図を見ながらｇｍに付いて説明していきます。
　実は、真空管のｒｅ（ｒｋと書いた方が良いでしょうか）は簡単には計算が出来ません。※１仕方がないので、もう一度トランジスタを振り返ってみたいと思います。
トランジスタでは　Ｇａｉｎ　＝　ｇｍ　Ｘ　ＲＬ　＝　（１　/　ｒｅ）　Ｘ　ＲＬ　でした。
では出力の電圧はどうなるのでしょうか？
出力電圧　＝　入力電圧　Ｘ　Ｇａｉｎ　＝　入力電圧　Ｘ　（（１　/　ｒｅ）　Ｘ　ＲＬ）
　　　　　　　＝　入力電圧　/　ｒｅ　Ｘ　ＲＬ　　・・・並べ替えただけ
これは、「入力電圧を抵抗ｒｅで割ることによって一度エミッタ電流に変換し、その電流（＝コレクタ電流）とＲＬを掛け算することで出力電圧が作られる」事を示しています。（１）で波形を計算した時もそうしていました。アナログ回路ではたいていの場合同じ考え方で増幅が行われます。とすると、入力電圧を例えば１Ｖ振ってコレクタ電流が何Ａ変わるか見れば真空管のｇｍも分かりますね。　次の図１，２を見てください。

※　トランジスタは電流駆動：電流出力で、評価指標（良いとか、良くないとか）のひとつにｈｆｅ（＝Ｉｃ/Ｉｂ）があります。ｒｅは前回の通りコレクタ電流で決まってしまいますからどんなトランジスタもほぼ同じ値となり評価指標としては使えません。勿論、ｈｆｅは設計売る際にも重要な値です。これに対し真空管やＪＦＥＴは電圧駆動：電流出力でありｈｆｅでは表現できず、ｇｍの指標がとても重要になってきますし、また、設計ではなくてはならない値です。

ｇｍ　＝　出力電流の変化量　/　入力電圧の変化量となります。
だから ｇｍ Ｘ ＲＬでＧａｉｎが出るし、ｇｍはエミッタ抵抗の逆数になるんですね。※２

※２　ここでは真空管のｒｐに付いて考慮していません。実際にはｇｍとＲＬだけでは正確にＧａｉｎは決まりません。興味のある方はｒｐに付いても調べてみてください。

真空管１２ＡＸ７の特性を見てみましょう

　図３は三極複合管１２ＡＸ７の　プレート電流：プレート電圧　特性です。
プレート電圧＝２５０Ｖ、プレート電流１ｍＡ付近でのｇｍを計算してみましょう。

図３

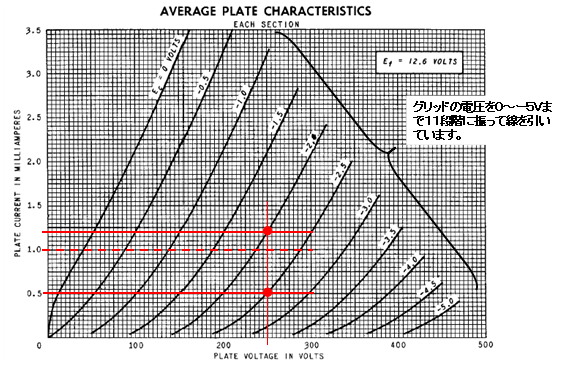
ｇｍ ＝ ⊿Ｉｐ / ⊿Ｖｇ ＝ （1.2mA – 0.5mA）/（2.5V – 2.0V） ＝ 1.4m MHO ＝ 1400u MHO

私が見たも資料ではｇｍが直読できるグラフも付いていましたので比べてみましょう。

図４

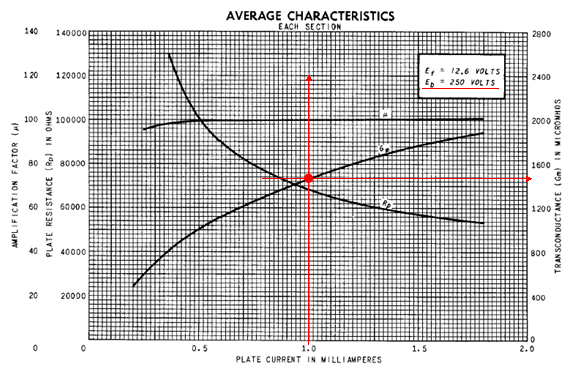
これを見ると、同じ条件でｇｍが1380u MHOと読み出せます。
先ほどの計算値とほぼ同じ値を示しました。
（このグラフではプレート電圧が２５０Ｖに限定されてしまう事に注意をお願いします。）

どうでしょうか？　ｇｍに付いて体感的に分かって頂けましたでしょうか。

補足：トランジスタの場合、現実にはｒｅをわざわざ逆数にしてｇｍとして使うことはほとんどなく、ｒｅを直接使って設計を行います。今回はｇｍを理解して頂く為にｒｅから説明してみました。真空管のカソードフォロアのインピーダンスは１/ｇｍで、トランジスタの考え方と同じになります。