真空管の交換時などで出てくるgmってなに?(1)
真空管の三定数として、μ(増幅率)、gm(相互コンダクタンス)、rp(プレート抵抗)があります。これらに付いて多くの方がWeb上でも説明してくれていますが、どうも体感的に理解できないという方もいるのではないでしょうか。今回はこの中のgmに付いて取り上げ、二回に亘って説明させてもらいます。そういう事だったのかと思っていただければ幸いです。
(1)では真空管ではなく、トランジスタで簡単なアンプを考えてみます。真空管が難しいという訳ではなく、その方が理解しやすいと考えたからです。その後、gmの考え方に付いて説明します。そして(2)でトランジスタと比較しながら真空管のgmに付いてお話しします。
突然ですが、私がいちばん最初にトランジスタを知った時、「hfeという特性があって、例えば入力であるベース電流に1μAの電流を流すと出力には100μAの電流が流れる(hfe=100)から、これで100倍のアンプが出来るんだ」と思っていました。一段の簡単なアンプでは、この値を直接には使いません。
トランジスタ一個でアンプを考える
では、トランジスタ一個と抵抗数個を使って一緒にアンプを設計するところからはじめてみましょう。
ここでトランジスタに付いてもう一度確認しておきます。図1を見てください。
(1) 三本の足があります。それぞれエミッタ、ベース、コレクタという名前です。
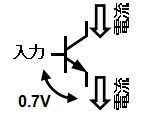
ここまでは、知っている方も多いと思います。次からです。図2を見てください。
(2) ベースは電圧を印可する端子(例外もあります)ですが、電流は流れません。
(3) エミッタには、ベースの電圧より0.7Vだけ低い電圧がいつも出ます。
(4) コレクタにはエミッタと同じ電流が流れます。電圧は他の端子と無関係です。
図1

図2
(2)(3)(4)の特徴を使って2倍のアンプが出来ないか、想像してみましょう。
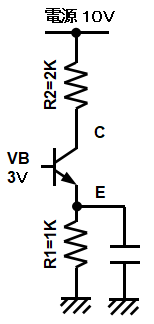
図3をご覧ください。抵抗を二本追加して、次のようにしたらどうでしょうか。抵抗値と電圧は、取り合えず私が決めてみました。
では、順を追って説明します。
使う知識は、オームの法則だけです。
まず入力のベース電圧(VB)を3Vにしました。エミッタの電圧(VE)は、ベースより0.7V低いので2.3Vになります。エミッタに流れる電流は2.3V/1KΩ=2.3mAとなります。コレクタに流れる電流は、エミッタに流れる電流とおなじですから2.3mAになります。最後にコレクタの電圧(VC)です。2KΩの両端の電圧が図の通り4.6Vですから、電源電圧10V-4.6Vで5.4Vになります。このコレクタの電圧が出力電圧になります。なんとなく2倍のアンプになっていると気が付かれた方もいらっしゃると思います。確認しみましょう。入力の電圧を±0.5V振ってみます。この様子を図4,5に示しました。
図3

図4

図5

図6
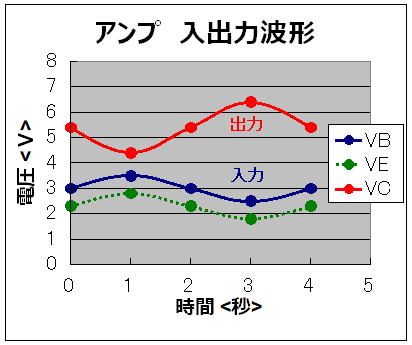
最初にVB(入力電圧)が3V、1秒後に3.5V、2秒後に3V、3秒後に2.5V、そして4秒後に3Vとなったとします。図3,4,5の結果を時系列に並べてみます。図6にその様子を示しました。
二倍のアンプが出来ているのが分かると思います。また、入力(VB)と出力(VC)が逆相になっている事や、1秒の時点で入力と出力の間の電圧に余裕の無い事も分かると思います。
そして、ここまで来るとこのアンプのゲインは R2/R1=2 で決まっていることも分かると思います。(Hfeを使った計算は出てきませんでしたね。)
理解いただいていると思いますが、0秒の時入力は3V、出力は5.4Vで、これをもってゲインは5.4V/3Vとはなりません。そうです、出力の変化量/入力の変化量になることに注意してください。
それから信号を入れる前のベース電圧を3Vとしました。この電圧を掛けることをバイアスを掛ける、そしてこの電圧をバイアス電圧と呼びます。真空管アンプでもバイアス調整の言葉で出てきますね。
トランジスタのgm
2倍のアンプが出来たところで、gmのお話しをさせてもらいます。下図7,8,9を見てください。バイアス電圧をどんどん下げていきます。電流とゲインは同じにしています。この調子でR1を0になるまで下げたらどうなるでしょう。実はR1が0になってもトランジスタの中の抵抗が残ります。配線などの物理的な抵抗でなく、ダイオードの非線形からくる抵抗で、re(スモール・アール・イー、またはエミッタ抵抗)と呼び、エミッタに外付けされた抵抗R1とは明確に区別します。話が別の方向に行ってしまうのでここでは詳細を略させてもらいますがその時は、ベース:エミッタ間電圧は0.7V一定でなくなり少し変化します。
図7

図8

図9

無理やり書けば、図10のようなイメージでしょうか。
トランジスターの場合、reの計算ができます。
re = 26mV / Ic ・・・・ Icはコレクタ電流を指します。
最初の回路(図3)では2.3mA流れていましたので、11.3Ωになります。R1が1Kでしたのでreは十分無視できると言えます。
ここでもう一つ。最初の回路では波形のグラフからゲインが上げられなかった(上げにくかった)ですよね。そこで、図11の様にエミッタにコンデンサを追加して(バイパスコンデンサと呼びます)信号が入ってもエミッタが動かないようしてしまいましょう。
これまでの説明からゲインは
Gain = R2 / re = 177倍 ※2
となります。
この式の中の 1 / re の事をgmと呼びます。
Gain = gm X R2 と書き換えることができます。
※2 トランジスタの中にも純粋な抵抗がありますから実際はもう少し小さな値になります。また、ゲインが高くなった分、入力を小さくするとか電源電圧を上げるとか、工夫が必要になります。
図10
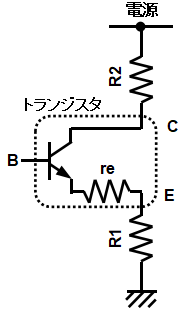
図11
ではここまでの結論です。
gmとはreの逆数です。・・・・トランジスタの場合
R1がない場合(コンデサを付けても良いですが)ゲインの計算は
Gain = (1/ re) X R2 = gm X RL (R2は負荷抵抗で記号でRLで表します)
gmが分かるとゲインを計算するときに便利ですよね。
長くなりましたが、次は真空管で説明させてもらいます。
(※ 説明の都合上、入力ダイナミックレンジ、飽和、RE(ラージ・アール・イー)、接地の形、耐圧、AC特性など、実際と異なるところや配慮すべきところがありますがご容赦願います)

